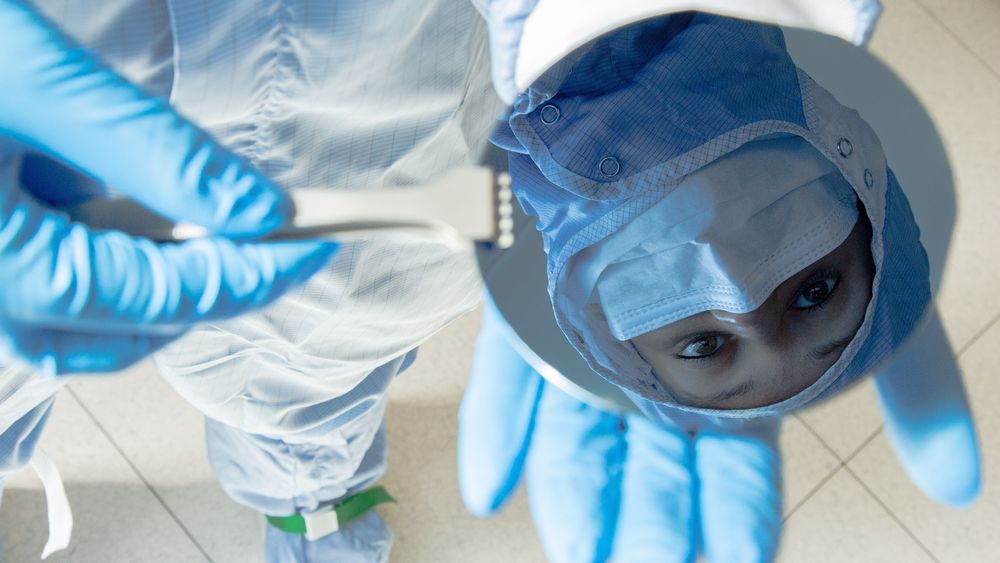
Denne artikkelen er levert av Titan.uio.no, en nettavis utgitt av Universitetet i Oslo (UiO).
Forskere legger nå grunnlaget for fremtidens kvantedatamaskiner ved å skyte vekk atomer.
Gled deg! I denne reportasjen kan du lese om hvordan forskere ved Universitetet i Oslo bombarderer solcellepanel-lignende materialer for å legge grunnlaget for det som kan bli fremtidens IT-revolusjon: selveste kvantedatamaskinen. Den er fundamentalt annerledes enn dagens datamaskiner.


For å henge med i svingene, og det vil jeg på det varmeste anbefale deg å gjøre, må vi underveis drøvtygge på noen merkverdige fenomener i den kvantemekaniske verden.
Færreste kjenner til
Så sett deg i godstolen, legg realfagsskrekken og utålmodigheten på hattehyllen og nyt den nye, spennende verden som åpner seg. Innen denne saken er ferdiglest, håper jeg at du har latt deg begeistre av en merkelig verden som de færreste av oss kjenner til i dag.
La oss starte med det helt elementære. Du er kanskje blant de heldige som drasser rundt på en bærbar PC?
Selv om den bærbare PC-en din kan gjennomføre flere milliarder regneoperasjoner i sekundet, er den ikke rask nok for de forskerne som må gjennomføre så omfattende beregninger at det kan ta flere år på en vanlig PC.
Ti tusen ganger raskere
En del løser problemene sine på tungregnemaskiner, som er opptil ti tusen ganger raskere enn en vanlig PC, men noen av regneproblemene deres er likevel så krevende at selv tungregnemaskinene må melde pass.
Et eksempel er når nye nanomaterialer med helt bestemte magnetiske og elektriske egenskaper skal designes. Det er forferdelig krevende, noe vi kommer tilbake til. Et annet eksempel er å knekke krypterte koder. Hvilken drøm når etterretningsvesenet skal dekryptere hemmelige meldinger fra folk med onde hensikter!
– Vi har allerede nådd grensen for hvor raske datamaskinene kan bli med dagens teknologi, forteller stipendiat Marianne Etzelmüller Bathen på Senter for materialvitenskap og nanoteknologi ved Universitetet i Oslo.
Må tenke nytt
Teknologene må derfor tenke nytt. Bathen har nå tatt i bruk avanserte, matematiske beregninger og intrikate, nanotekniske eksperimenter for å designe grunnlaget for fremtidens kvantedatamaskiner.
Akkurat som dagens datamaskiner er satt sammen av bits, som enten kan ha verdiene 0 eller 1, blir kvantedatamaskinene bygd opp av kvantebits.
Med to bits får du de fire ulike kombinasjonene 00, 01, 10 og 11. Med tre bits har du åtte ulike kombinasjoner, og med åtte bits har du 256 ulike kombinasjoner. Du trenger derfor åtte bits for å kunne skille mellom 256 tegn. Dette er grunnpilaren i dagens datamaskiner.
Uendelig antall verdier
Det betyr: Én enkelt bit kan bare ha to ulike verdier. En kvantebit kan derimot ha et uendelig antall verdier.


– Du kan sammenligne en kvantebit med en pendel. I en pendel har du én tilstand på venstre side og en på høyre side, men ettersom pendelen svinger frem og tilbake, har du også mellomtilstander.
Det som er så spesielt, er at du ikke vet hvor pendelen er. Selv om verdiene til kvantebitsene er usynlige, ja, du leste riktig, kan forskerne utnytte denne usynlige egenskapen til å gjøre beregninger med enormt store tall med tusenvis av sifre.
– Det rare med kvantemekanikken er at du ikke vet om du har en tilstand som er «på» eller «av» eller noe «midt imellom», men du kan regne ut sannsynligheten for de ulike tilstandene.
20 kvantebits
– Dette er den enkleste forklaringen på at kvantedatamaskiner kan være raskere enn vanlige datamaskiner. En kvantebit kan være på og av på samme tid. Eller noe midt imellom. Du har alt samtidig, forteller Bathen.
Den første kvantedatamaskinen finnes allerede. IBM har en kvantedatamaskin med 20 kvantebits. Google planlegger nå en kvantedatamaskin med 72 kvantebits. Allerede med så få kvantebits skal den kunne regne raskere enn det verdens raskeste maskin klarer i dag.
En kvantedatamaskin med så mye som 10 000 kvantebits kan gjøre underverker.
– Poenget med kvantedatamaskiner er å bruke dem til å løse matematiske oppgaver som vanlige datamaskiner ikke klarer, slik som å faktorisere store tall. De vil være spesielt gode til sannsynlighetsberegninger, poengterer Etzelmüller Bathen.
Utnytter elektroner og atomer
Kvantebits kan lages ved å utnytte egenskaper i elektroner, atomkjernen eller lyspartikler. Denne saken handler om hvordan elektroner kan brukes til kvantebits.
Jo kaldere kvantebitsene er, desto mindre beveger elektronene seg. Da er det lettere å få kontroll på dem. For at disse kvantebitsene skal fungere, må temperaturen derfor holdes så lav som mulig.
Her snakker vi om noe så bitende kaldt som minus 270 grader. Det er bare noen grader over universets absolutte nullpunkt. Da er det ikke så rart at disse kvantebitsene blir svært dyre og vanskelige å produsere.
Mulig å få det billigere?
Nanoteknologi-gjengen ved Universitetet i Oslo forsker nå på om det er mulig å lage billige kvantebits som også fungerer i romtemperatur.

Hele ideen bygger på forskningen til nylig avdøde professor Bengt Svensson på Fysisk institutt ved UiO. Han har i en årrekke ledet en svær forskningsgruppe for å designe verdens mest effektive solceller. Marianne Etzelmüller Bathen er en del av denne gruppen.
Den store utfordringen deres har vært å finne frem til solceller med den mest optimale kombinasjonen av grunnstoffer. Alle eksperimentene skjer på Mikro- og nanoteknologilaboratoriet, et hypermoderne laboratorium eid av UiO og Sintef.
Defekte materialer
Eksperimentene er naturlig nok ikke alltid like vellykket. Nanoforskerne har bommet en rekke ganger. Det er en del av forskningens natur. Da blir ikke materialene som de skal.
– Før ble defekte materialer sett på som dårlige. Nå utnytter vi disse feilene til å lage noe som virker, forteller Bathen.
Det viser seg at en bestemt type defekt materiale med noen ørsmå endringer kan fungere som innmaten i en kvantedatamaskin. Og med ørsmå endringer mener vi noen små endringer helt nede på atomnivå.
Mens de fleste solceller består av silisium ispedd noen andre grunnstoffer her og der, har Senter for materialvitenskap og nanoteknologi i en årrekke også forsket på silisiumkarbid.
Hardt som diamant
Materialet er ikke giftig, brukes en del i elektronikk og er nesten like hardt som diamant. Det er smart, da går det ikke så lett i stykker. Materialet er dessuten lett tilgjengelig.
– Industrien vet hva dette er, så hvis silisiumkarbid skulle bli aktuelt til kvantedatamaskiner, er det lett for dem å endre produksjonen, poengterer Marianne Etzelmüller Bathen.
En av hennes mange utfordringer er at materialet må ha et helt bestemt båndgap. Båndgapet sier noe om hvor mye energi som må til for å få tak i elektroner.
Regelen er svært enkel: Materialer uten båndgap leder strøm. Materialer med stort båndgap leder ikke strøm. Halvledere er materialer med et båndgap midt imellom. De leder bare delvis strøm.
Naboatomer
Materialet hennes er bygd opp på en helt bestemt måte. Hvert av atomene har fire naboatomer. Atomene samarbeider om elektronene mellom dem.
For å lage kvantebits, bombarderer hun materialet med protoner. Når protonene kolliderer med atomer inne i materialet, har de noen ganger nok energi til å dytte vekk atomer fra plassen deres.
– Ved å styre hvor raskt jeg skyter inn protonene og hvor mange av dem jeg skyter inn, kan jeg bestemme hvor mange atomer som skal dyttes vekk. Jeg kan også styre hvor dypt inne i materialet atomene skal fjernes.
Og det er her vi kommer til et viktig poeng.
Kvantebitsene hennes befinner seg i de tomme plassene der atomene er fjernet. Fysikerne kaller disse tomme plassene for vakanser, et fisefint ord for «ubesatt» eller «ledig». Vakanser er altså de områdene i et materiale som mangler atomer.
– Du kan sammenligne dette med å gå i en hall med mange tykke stolper som holder taket oppe. Tenk deg at stolpene er atomkjerner og menneskene i hallen er elektroner. Menneskene må naturlig nok gå mellom stolpene. Det blir mer plass der det mangler en stolpe. Da vil menneskene samle seg der.
Det er omtrent det som skjer når du fjerner atomer; det ledige området vil trekke til seg elektroner. Og det er nettopp det som er poenget i en kvantebit.
Alt dette er kvantebit
I utgangspunktet er som sagt hvert atom bundet til fire andre atomer. Mellom to og to atomer er det fire elektronpar, altså åtte elektroner tilsammen.
– Når jeg fjerner ett atom, har jeg fire elektroner til overs. Disse fire elektronene blir lokalisert rundt den ledige plassen. Noen ganger kan den ledige plassen binde til seg enda noen elektroner, og noen ganger kan de ekstra elektronene forsvinne. Ved å sette på elektriske felt kan jeg bestemme hvor mange elektroner som skal være i den tomme plassen.
Og det som er så ufattelig: Disse elektronene kan være en kvantebit.
I materialet hennes er annethvert atom silisium og annethvert karbon. Det betyr: Rundt hvert silisiumatom er det fire karbonatomer, og rundt hvert karbonatom er det fire silisiumatomer.
Selv om hun skyter ut både karbon- og silisiumatomer, er det bare de tomme silisiumplassene som fungerer som kvantebits.
«Snakker» til atomene
Forklaringen er enkel. Silisiumatomer er tyngre enn karbonatomer. Når man fjerner et karbonatom, vil silisiumatomene rundt dette karbonatomet flytte på seg. Det påvirker energien i den tomme karbonplassen.
Når man derimot fjerner et silisiumatom, vil karbonatomene rundt dette silisiumatomet ikke flytte like mye på seg. Da vil elektronene til den tomme silisiumplassen ha andre energier.
Det er ikke mange tomme atomplasser i materialet hennes. For hver av de tomme atomplassene er det mer enn én milliard vanlige atomer.
– Vi kan faktisk «snakke» til hver enkelt tomme atomplass ved å sende laserlys inn i materialet mitt.
Utrolig presisjon
Kvantebitsene hennes har et helt spesielt optisk «fingeravtrykk». Det betyr at når hun sender laserlys inn i materialet, vil elektronene i den tomme plassen få mer energi. Når elektronene gir tilbake energien sin, vil de gi fra seg et lysfoton. Dette er lys med en helt spesifikk bølgelengde.
– Hvert elektron sender bare ett lysfoton om gangen, og det er disse lysfotonene jeg leter etter. Jeg kan da måle om jeg har funnet en tom silisiumplass, se hvor mange elektroner som er der og hvilken energi de har.
– Det betyr at jeg kan snakke med og sende signaler til og fra hver enkelt kvantebit, og når de etterhvert snakker sammen, kan jeg påvirke hva de gjør, poengterer Bathen.
Det at hun klarer å finne en tom atomplass med laseren, er egentlig like utrolig som om hun skulle ha funnet frem til en helt bestemt person i Kina bare ved å lytte etter stemmen hans.
Bathen har også muligheten til å måle antall tomme atomplasser i materialet. Ved å sette på et magnetfelt, kan hun styre hvilke fotoner, altså lyspartikler, som de tomme atomplassene skal sende ut. Magnetfelt kan dessuten være nøkkelen til at kvantebitsene skal kunne snakke sammen.
Selv om Bathen ikke forsker på å sende informasjon mellom kvantebitsene, kan det likevel tenkes at kvantebitsene hennes påvirker hverandre.
– Jeg jobber med å kontrollere hvor mange jeg klarer å lage, og jeg prøver å finne ut av hvor nær de må være for at de skal kunne snakke med hverandre – og hvor langt unna de må være for at de ikke skal snakke sammen.
–Poenget er altså å kunne forstå hvordan kvantebitsene er plassert i forhold til hverandre og i hvilken grad de kommuniserer.
Spinnvilt

En av de store oppgavene hennes er å se hvilken type hulrom hun har laget, hvor mange elektroner som er bundet til dem og tilstanden til elektronene.
Det skal vi forklare nærmere. Som du leste tidligere i denne saken, kan en kvantebit være på og av på samme tid. Eller noe midt imellom. Samtidig.
For alle som ikke lever i den kvantemekaniske verden, høres dette forferdelig rart ut. Hokuspokuset handler om at alle elektroner har en spinntilstand. Spinntilstanden er usedvanlig viktig i kvantebitsenes verden. Forklaringen på dette merkverdige fenomenet er spinnvill.
– Begrepet er ikke mulig å forklare med klassisk fysikk. Spinn er en innebygd egenskap i elektroner, men spinn er likevel ikke en bevegelse. Elektroner kan ta to ulike typer spinn, opp eller ned. Selv om dette er en matematisk idé, kan vi forenklet si at elektroner roterer rundt sin egen akse, men rotasjonen er likevel annerledes enn i den rasjonelle verden.
Roterer to ganger rundt aksen
Elektroner må rotere to ganger rundt sin akse for å komme tilbake til utgangspunktet. Elektroner har spinn både når de går rundt kjernen og rundt sin egen akse.
Ett enkelt elektronspinn kan altså ha verdien opp eller ned eller noe midt imellom. Denne verdien kalles en superposisjon.
– Det rare med elektronspinnet er at det likevel bare kan observeres med de to ulike verdiene, opp eller ned. Opp og ned kan representeres med tallene 0 eller 1. Det betyr at uansett hvilken tilstand elektronspinnet har, vil spinnet, når det måles, bare gi svarene 0 eller 1.
– Begge tilstandene er til stede inntil tilstanden måles. Så selv om informasjonen er der, er den ikke fullt tilgjengelig for oss. Det gjør det vanskelig å måle hva som skjer når en kvantedatamaskin jobber. Den fungerer sånn sett helt annerledes enn hva man er vant til å tenke om en klassisk datamaskin, forteller professor i kvantefysikk Joakim Bergli på Fysisk institutt ved UiO.
Sender superposisjon
Han påpeker at det ikke er mulig å hente ut all informasjon i kvantedatasystemer.
– Det er noe av hemmeligheten, men du kan likevel løse dette om du gjør det riktig. I teorien kan man faktisk få uendelig mye informasjon i en kvantebit.
For å illustrere problemet med hvordan du kan avsløre verdien i en kvantebit, kan du gjennomføre et tankeeksperiment. Tenk deg at du har en tildekket boks, der du legger inn tre tall etter hverandre.
Hvert av de tre tallene er 0 eller 1. Det betyr at du kan legge inn de åtte mulige kombinasjonene 000, 001, 010 og så videre til 111. Boksen spytter ut et tall avhengig av hvilke tall som kommer inn.
– Så sier jeg til deg: Jeg vet hvordan denne boksen virker, men vil ikke dele hemmeligheten med deg.
Du må altså selv finne ut av hva boksen svarer. Halvparten av gangene svarer den 0 og resten av gangene 1. Men hvorfor den noen ganger svarer 0 og andre ganger 1, må du selv finne ut av.
Dette kan løses ved å gjenta forsøket en rekke ganger. Med en klassisk datamaskin er dette den eneste muligheten.
– Med en kvantedatamaskin kan vi sende inn en superposisjon av alle de åtte mulighetene på én gang. Svaret blir da en superposisjon av alle de åtte verdiene som kommer ut.

– Løst for visse problemer
Selv om en kvantebit altså kan inneholde alle mulige varianter mellom 0 og 1, returnerer den bare 0 eller 1. Du må derfor finne et lurt triks for å fravriste den hemmelige verdien til kvantebiten.
– Dette trikset er løst for visse problemer, slik som for dette eskeproblemet.
Selv om du måler at elektronspinnet får verdien 0 eller 1, vil du, når du måler elektronspinnet mange nok ganger, få et snitt du kan bruke.
– I den klassiske, fysiske verden er vi vant til determinisme. I kvantemekanikken er det derimot tilfeldighetene som rår. Du risikerer at du får et svar som du ikke kan bruke, men hvis du gjentar spørsmålet mange nok ganger, får du rett svar. Så sjansen for feil er i praksis så liten at det ikke er noe problem, påpeker Joakim Bergli.
Ikke sikkert det går fortere
Selv om du skulle finne en effektiv algoritme på kvantedatamaskinen, er det likevel ikke sikkert at beregningene dine går fortere på en kvantedatamaskin.
Hvis du skal faktorisere et tall, slik som at 56 = 2 x 2 x 2 x 7, vil denne beregningen gå langt raskere på en klassisk maskin. Poenget er at tiden for hvor lang tid en beregning tar, øker raskere på en klassisk maskin enn på en kvantedatamaskin. Det betyr at en kvantedatamaskin kan vinne temporittet hvis tallet er stort nok.
Det å faktorisere store tall er viktig for dem som forsker på sikkerhet, men Joakim Bergli påpeker at det ikke akkurat er samfunnsmessig produktivt å knekke koder.
– Kvantedatamaskinene er derimot svært nyttige om du skal lage nye materialer med nye egenskaper, slik som materialer med helt bestemte magnetiske egenskaper ved ulike temperaturer.
Klarer ikke nedkjølingen
Alle magneter som varmes opp, vil etterhvert slutte å være magnetiske. Forklaringen er at elektronene beveger seg for mye i sterk varme.
Da klarer ikke elektronene lenger å gå i takt. Når materialet kjøles ned, vil de bli magnetiske igjen.
– Selv om dette prinsippet er forstått, er det vanskelig å beregne overgangen fra en magnetisk til en ikke-magnetisk tilstand.
Bergli trenger også kvantedatamaskinen til å studere de elektriske egenskapene i materialer.
– Da kan vi få mer kontroll på hvordan vi bygger opp materialer med helt spesielle elektriske og magnetiske egenskaper, poengterer han.