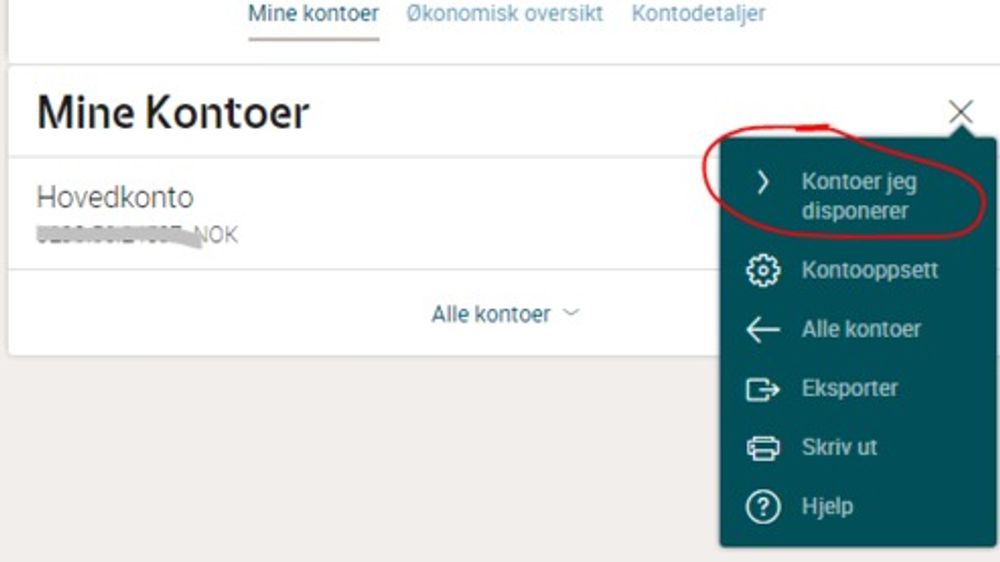
I forrige uke skrev blant annet VG og NRK om Stig Rovik som fikk sjokk da han sjekket nettbanken. Der stod det nemlig 21 474 836,47 kroner disponibelt på konto.
Rovik syntes det var rart at han ikke hadde hørt noe fra Hamar, da han hadde spilt både Vikinglotto- og Lotto-kuponger. «Mangemillionæren» skjønte fort at noe var feil, og kontaktet banken sin som kunne fortelle ham at pengene aldri hadde stått på konto.
Feil hos flere
Det var bare en feil i bankappen - som hadde dukket opp hos flere Sparebank-kunder.
For de fleste av oss er 2147483647 bare et stort tall, men en utvikler vil straks kjenne igjen tallet som det åttende Mersenne-primtall.
Det er det største heltallet en datamaskin klarere å presentere med ett og null før den får en «overflow».
Største primtallet
Siden 2147483647 er det største heltallet en datamaskin klarerer å presentere, er det relativt vanlig å bruke det til testdata, forklarer programmerer Per-Frode Pedersen i konsulentselskapet Bouvet til NRK.
– Det er et lett tilgjengelig tall hvis du for eksempel skal lage skjermbildeeksempler. Jeg bruker det ofte i jobben min, sier Pedersen til NRK.
Pedersen mener glippen i bankkappen skyldes at noen må brukt 2147483647 som testdata i utviklingen av mobilappen.
Brukt som testdata
Det bekreftes av informasjonsdirektør Sigurd Ulven i Eika Gruppen som eier Sparebankene.


– Jeg fikk melding fra de danske utviklerne våre at dette var et tall en tidligere utvikler hadde brukt, sier han til NRK.
I 1772 var 2147483647 (tilsvarende 231-1) det største primtallet vi kjente til. Det ble oppdaget av den tyske matematikeren Leonhard Euler.
I 1811 skrev Peter Barlow at tallet antageligvis var det største primtallet som noen gang kom til å bli oppdaget.
274,207,281-1 er største primtallet vi kjenner til
Lite visste han da at interessen for primtall skulle eksplodere i fremtiden.
I dag er det største primtallet vi kjenner til 274,207,281-1. Tallet har 22 338 618 sifre, og ble oppdaget av amerikaneren Curtis Copper 7. januar 2016.
Tallet ble funnet gjennom samarbeidsprosjektet Great Internet Mersenne Prime Search (GIMPS).
Selv om primtall har stor verdi innenfor kryptografi, er 274,207,281-1 for stort til å ha noen praktisk verdi.